判断平面内点在多变形内外的射线算法及实现

  algorithm
  14 minutes read (About 2105 words)

判断一个点是否在多边形内&GIS LBS 系统中的应用说明

如何判断一个点是否在多边形内部？

  1. 面积和判别法：判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形，相等则在多边形内部。
  2. 夹角和判别法：判断目标点与所有边的夹角和是否为360度，为360度则在多边形内部。
  3. 引射线法：从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。

1.2.都非常好理解，但是1.2. 并不适合所有的多边形，比如说凹多边形。关于射线算法，好像没有公式证明，不过网上很多论文可以google到.

实例一
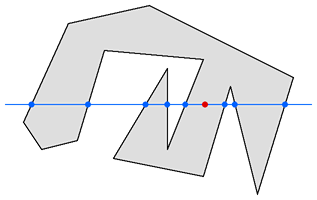
图一：点延伸出的射线穿过不规则多边形，往左射线交5点，往右射线交3点，所以判断点在多边形内

多边形要规避一些极端情况，比如自我闭合等情况，具体可以参考Determining Whether A Point Is Inside A Complex Polygon

关于GIS/LBS上的应用，问，该算法是否可以判断经纬度坐标是否在一个标记的地图围栏中（任意多边形）,答案是可以，但是需要注意两个问题：

  1. 如果你的多边形有一个在地球上穿越一个大距离的单侧，那么多边形中的点将沿着一条明显弯曲的路径朝那个方向（特别是靠近两极），而不是一个真实的，最短的距离路径。如果你的多边形没有一个侧面穿过很远的距离，你就可以避免这个问题
  2. 如果你的多边形穿过国际日期变更线，然后算法都会经突然重置完全乱了。它可能需要添加或减去360°一些点的经度来防止这种情况的发生。（但如果多边形完全围绕南北极，这个解决办法就行不通了。）

也就是地图是球形的，而且经纬度是对标国际日期变更线设定，这两个原因导致多边形最终并不处于一个平面坐标内。所以如果应用在中国一定规模区域范围内（比如汽车、自行车的活动范围），完全没问题。在中联，我们就将其广泛应用到一系列车辆产品上，例如 中联环卫车、餐厨回收车、搅拌车、泵车、干粉运输车等等，用来判断车辆是否驶离/驶入工厂工地和监控车辆是否处于合理范围内/外

文章包括三部分

  1. 算法原理
  2. 代码实现（csharp)
  3. 实际应用举例对比（图）

算法

从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部

代码实现（csharp)

几年前用 c# 封装的一个关于地图的工具包，包含 道格拉斯普克抽稀算法-用于 历史轨迹回放；点面射线算法-用于电子围栏，判断点是否在不规则平面多边形内；各种地图的经纬度纠偏-用于火星坐标和真实坐标的转换（可能存在最近几年地图供应商算法已经改变了）；下面给出平面内点在复杂多边形内外的射线算法，上一篇给到用于gis 系统中的轨迹回放，下一篇几个地图服务商的经纬度纠偏算法；

工具包源码已开源到github

还是坐标对象GeometryModels，包含点，线，多边形的定义

GeometryModels.cs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using System;
using System.Collections.Generic;
using System.Linq;
using System.Web;

/**
* GeometryModels 坐标对象
* shenlongguang
* https://github.com/ifengkou
*/
namespace L.MapUtil
{
    public enum TransType
    {
        Baidu,
        Mapbar,
        Mars
    }

    public class GeometryModels
    {
    }
    //点
    public class Point
    {
        public double X { set; get; }public double Y { set; get; }
        public Point(double x, double y) { this.X = x; this.Y = y; }
        public Point() { }
    }
    //线
    public class Line
    {
        public Point a { set; get; }public Point b { set; get; }
        public Line(Point start, Point end) { this.a = start; this.b = end; }
    }
    //多边形
    public class Polygon
    {
        public List<Line> Plines { get; set; }
    }
}

PolygonUtil.cs ，射线算法的实现，其中有考虑到算法的优化，和几种特殊情况的规避（如点在边上），注释还算详细，就不多解释

PolygonUtil.cs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

using System;
using System.Collections.Generic;
using System.Linq;

/**
* 判断平面内点在多变形内外的射线算法实现
* shenlongguang
* https://github.com/ifengkou
*/
namespace L.MapUtil
{
    class PolygonUtil
    {
        private static double minv = 1e-9;
        private static double maxv = 1e9;

        public static bool IsPointInPolygon(Point point, Polygon polygon)
        {
            int count = 0;
            //优化，判断点是否在多边形的外切矩阵内，如果不在可以直接跳过，减少计算
            if (IsPointInMaxMatrix(point, GetAllPointFromPolygon(polygon)))
            {
                var _line = new Line(point, new Point(-maxv, point.Y));
                foreach (Line l in polygon.Plines)
                {
                    //与x平行的边，则不做考虑。因为从点出发到负无穷的射线要么无交点，要么重叠。它仍然符合奇数在内，偶数在外的规则
                    if (l.a.Y != l.b.Y)
                    {
                        //判断点是否在多边形任意边上，true则判断为在其中
                        if (IsPointOnLine(point.X, point.Y, l.a.X, l.a.Y, l.b.X, l.b.Y))
                        {
                            return true;
                        }
                        //构建射线 _line = new Line(point, new Point(minv, point.y))
                        if (IsIntersect(l, _line))
                        {
                            //如果相交
                            count++;
                            //如果多边形的边的较小的一个端点在这条射线上
                            if (Math.Min(l.a.Y,l.b.Y) == point.Y)
                            {
                                count--;
                            }
                        }
                    }
                }
                return count % 2 == 0 ? false : true;
            }
            return false;
        }
     
        // 判断两线段是否相交
        private static bool IsIntersect(Line line1, Line line2)
        {
            //基本思想：线段1的两端点在线段2的两侧，线段2的两端点也分布在线段1的两侧，则判断为有交点
            return CheckCrose(line1, line2) && CheckCrose(line2, line1);
        }
        // 判断线段2是否在线段1的两侧
        private static bool CheckCrose(Line line1, Line line2)
        {
            Point v1 = new Point(line2.a.X - line1.b.X,line2.a.Y - line1.b.Y);
            Point v2 = new Point(line2.b.X - line1.b.X,line2.b.Y - line1.b.Y);
            Point v3 = new Point(line1.a.X - line1.b.X,line1.a.Y - line1.b.Y);
            return (CrossMul(v1, v3) * CrossMul(v2, v3) <= 0);
        }

        // 计算两个向量的叉乘。 
        private static double CrossMul(Point pt1, Point pt2)
        {
            return pt1.X * pt2.Y - pt1.Y * pt2.X;
        }
        private static HashSet<Point> GetAllPointFromPolygon(Polygon polygon)
        {
            //考虑采用set，不允许重复项。用list会有近1倍的重复数据（2n-1）
            HashSet<Point> lst = new HashSet<Point>();
            foreach (Line line in polygon.Plines)
            {
                lst.Add(line.a); lst.Add(line.b);
            }
            return lst;
        }
       
        //叉积 判断三点是否在同一直线上
        private static double Multiply(double px0, double py0, double px1, double py1, double px2, double py2)
        {
            return ((px1 - px0) * (py2 - py0) - (px2 - px0) * (py1 - py0)); //在一条直线上返回值为0 
        }
        //判断 点p0是否在线上p1-p2
        private static bool IsPointOnLine(double px0, double py0, double px1, double py1, double px2, double py2)
        {
            return (Math.Abs(Multiply(px0, py0, px1, py1, px2, py2)) < minv) && ((px0 - px1) * (px0 - px2) <= 0) && ((py0 - py1) * (py0 - py2) <= 0);
        }  
        //1、判断点是否在任意多边形的外切矩阵内,减少内部复杂运算几率
        private static bool IsPointInMaxMatrix(Point p, HashSet<Point> l)
        {
            return p.X<=l.Max(e => e.X)&&p.X>=l.Min(e => e.X)&&p.Y<=l.Max(e => e.Y)&&p.Y>=l.Min(e => e.Y);
        }
    }
    
}

实际应用

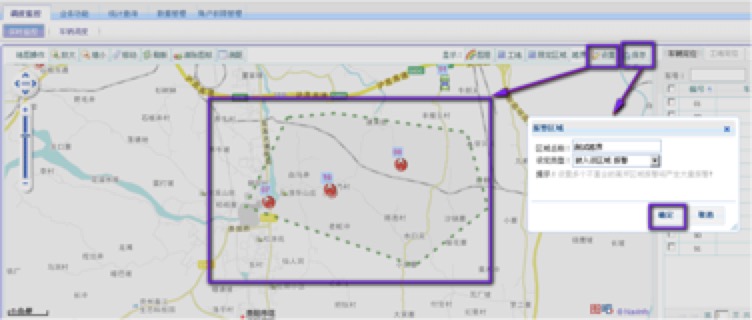
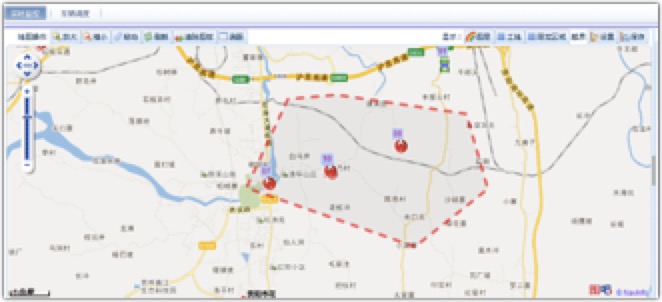
以中联搅拌车调度系统的电子围栏功能为例（环卫车、餐厨垃圾回收车、泵车、干粉砂浆运输车、罐等等都有应用，只是年代久远找不到几个截图了…)。因为搅拌车的活动轨迹，一般处于以搅拌站为中心，周边50公里范围内。作用在于1)判断车辆是否离场; 2)车辆是否进入工地（同时可以统计在途时间）; 3)车辆是否进入活动禁区（比如白天进x环，城市管理条例。。。）; 4)车辆是否驶离活动范围

时代久远，没找到图了，只好在用户手册中截取…


参考

参考：Determining Whether A Point Is Inside A Complex Polygon

  , 
经纬度纠偏
道格拉斯-普克抽稀算法

Comments

  Follow
Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×